Solution:
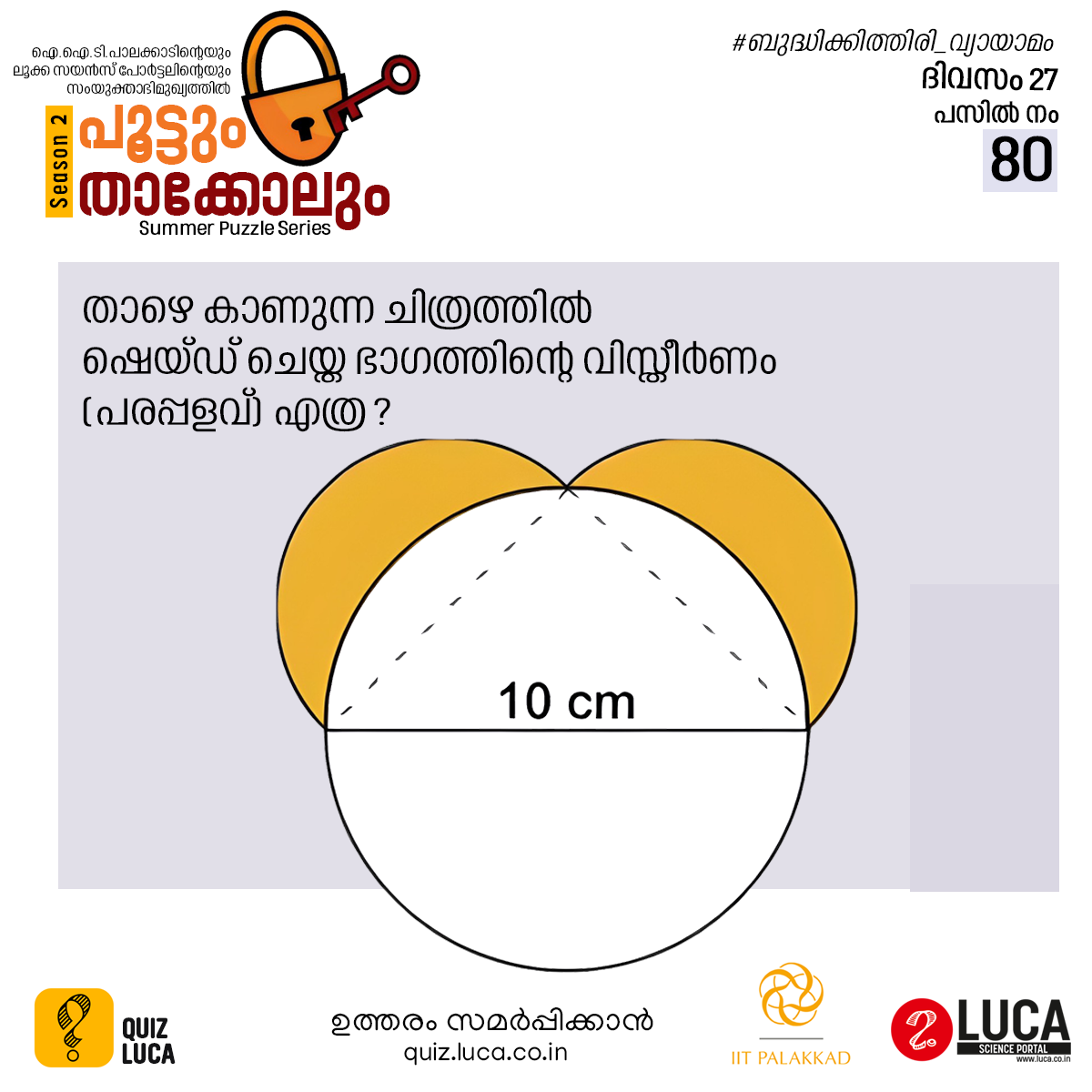
AB വൃത്തത്തിന്റെ വ്യാസമാണ് . അതുകൊണ്ടു C ഒരു മട്ടകോൺ ആണ്. ACB ഒരു മട്ടത്രികോണവും .
പൈതഗോറസ് തിയറം ഉപയോഗിച്ചാൽ
AB യുടെ മേലുള്ള അർദ്ധവൃത്തത്തിന്റെ വിസ്തീർണം = ACക്ക് മേലുള്ള അർദ്ധവൃത്തത്തിന്റെ വിസ്തീർണം + BCക്ക് മേലുള്ള അർദ്ധവൃത്തത്തിന്റെ വിസ്തീർണം.
ഈ അർദ്ധവൃത്തങ്ങളുടെ വിസ്തീർണത്തിൽ നിന്നും AC, BC എന്നീ ഖണ്ഡങ്ങളുടെ വിസ്തീർണങ്ങളുടെ തുക കിഴിച്ചാൽ മട്ടത്രികോണം ACB യുടെ വിസ്തീർണം കിട്ടും.
അതായതു ഷെയ്ഡ് ചെയ്ത ഭാഗങ്ങളുടെ വിസ്തീർണം = മട്ടത്രികോണം ACB യുടെ വിസ്തീർണം = ½ x 10 x 5 = 25cm2.
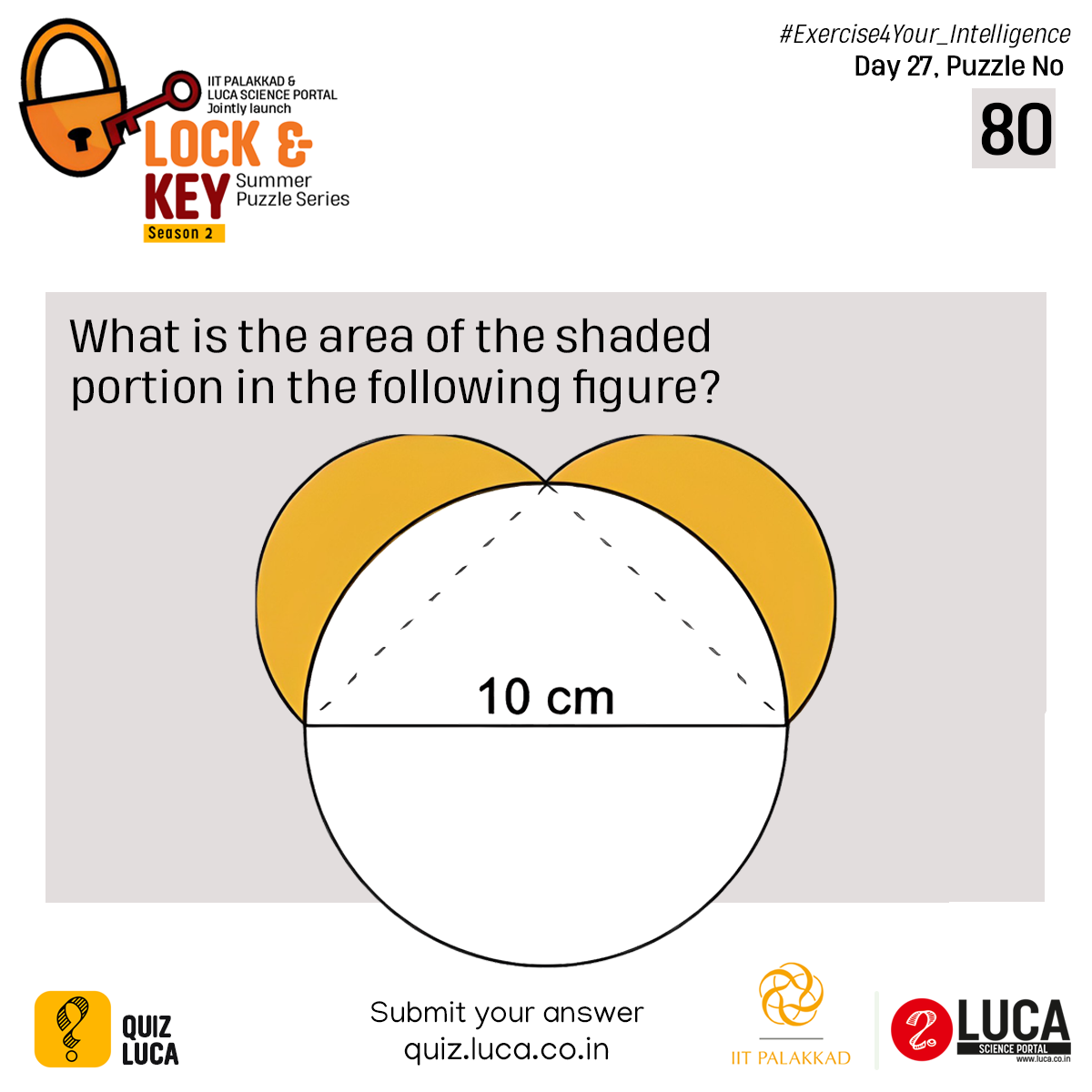
B is the diameter of the circle and so C is an angle in a semicircle, and therefore a right angle.
Using a generalisation of the Pythagoras theorem,
area of the semicircle on AB = area of semicircle on AC + area of semicircle on BC
Subtracting sum of area of the segments on AC and BC from both sides,
Area of Rt triangle ACB = sum of area of the lunes shaded.
Therefore the shaded area = ½ 10 x 5 = 25cm2.
| Attempts | 38 |
| Correct | 12 |
| Best Explanation | _ |
First 10 Correct Answers
| Sl No | Primary | High School | Others |
| 1 | Aman V Shankar | ഭഗത് സി ലതീഷ് | Athira R P |
| 2 | _ | Revathi. K | Aneesh Madathara |
| 3 | _ | Aadidev p | Aswini.R |
| 4 | _ | Geofferin George Saji | Pranav D P |
| 5 | _ | Franklin Joseph Saji | Dhanu |
| 6 | _ | _ | Umesh P Narendran |
| 7 | _ | _ | _ |
| 8 | _ | _ | _ |
| 9 | _ | _ | _ |
| 10 | _ | _ | _ |
