

Solution:
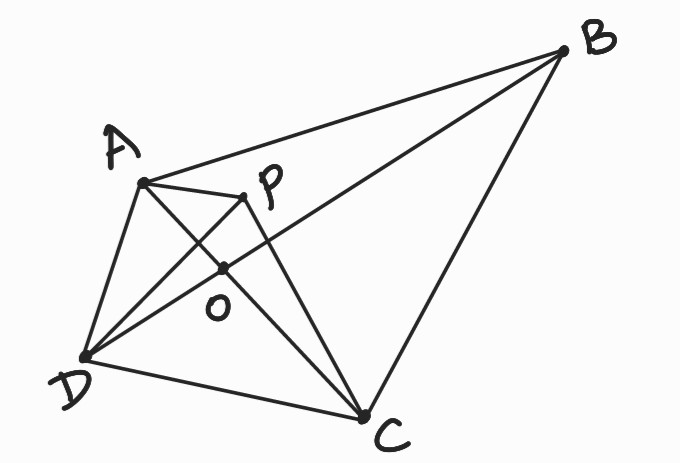
ഒരു ചക്രീയ ചതുർഭുജത്തിന്റെ വികർണങ്ങൾ അതിന്റെ ഉള്ളിലെ ഒരു ബിന്ദുവിൽ മുറിച്ചികടക്കുന്നു. ഈ ബിന്ദുവിനെ O എന്ന് വിളിക്കാം. A , B , C , D ചതുർഭുജത്തിന്റെ ശീർഷങ്ങൾ ആണ്. O ഇൽ നിന്ന് ശീർഷങ്ങളിലേക്കുള്ള ദൂരങ്ങളുടെ ആകെത്തുക d എന്നിരിക്കട്ടെ. d = OA + OB + OC +OD = AC + DB
P എന്ന മറ്റൊരു ബിന്ദുവിൽ നിന്ന് ശീർഷങ്ങളിലേക്ക് ഉള്ള ദുരങ്ങളുടെ ആകെത്തുക D എന്നിരിക്കട്ടെ.
D = PA + PB + PC + PD
ചിത്രത്തിൽനിന്ന്
PA + PC > AC
PB + PD > BD
PA + PB + PC + PD > AC + BD
അതായതു
D, dയെ കാൾ ഒരിക്കലും ചെറുതാക്കാൻ പറ്റില്ല. Pഉം Oഉം ഒരേ ബിന്ദുവായാൽ Dഉം dഉം രണ്ടും സമമാകും.
അപ്പോൾ മീറ്റിംഗ് ചക്രീയ ചതുർഭുജത്തിന്റെ വികർണങ്ങൾ മുറിച്ചുകടക്കുന്ന ബിന്ദുവിലായിരിക്കണം.
Since the quadrilateral is a convex set, the diagonals intersect at some interior point 𝑜.
Suppose that the vertices of the quadrilateral are 𝐴, 𝐵,𝐶 and 𝐷. The the sum of distance from o to the vertices is equal to 𝐴𝐶 + 𝐵𝐷. But forany other point 𝑃,
𝑃𝐴 + 𝑃𝐶 > 𝐴𝐶.
Similarly 𝑃𝐵 + 𝑃𝐷 ≥ 𝐵𝐷. This means that the sum of distances from 𝑃 to the vertices is not less that 𝐴𝐶 + 𝐵𝐷
and this sum is equal to 𝐴𝐶 + 𝐵𝐷 if and only if 𝑃 coincides with the point 𝑂.
So the minimum sum of distances of a point from the vertices is AC + BD.
Therefore the meeting has to be at the point of intersection of the diagonals
Best Explanation : Umesh P Narendran
A, C എന്ന രണ്ടു ബിന്ദുക്കളെടുക്കുക. അവ തമ്മിലുള്ള ഏറ്റവും കുറഞ്ഞ ദൂരം അവയെ യോജിപ്പിക്കുന്ന രേഖാഖണ്ഡം ആണ്. ഈ രേഖാഖണ്ഡത്തിലെ ഏതു ബിന്ദു എടുത്താലും അതിൽ നിന്ന് ഈ രണ്ടു ബിന്ദുക്കളിലേക്കുമുള്ള ദൂരങ്ങളുടെ തുക ഏറ്റവും കുറവായിരിക്കും. വേറേ ഏതു ബിന്ദു എടുത്താലും triangular inequality അനുസരിച്ച് ദൂരം അതിനേക്കാൽ കൂടുതലായിരിക്കും.
അതു പോലെ B, D എന്നീ ബിന്ദുക്കളിലേക്കുള്ള ദൂരങ്ങളുടെ തുക ഏറ്റവും കുറവ് അവയെ യോജിപ്പിക്കുന്ന രേഖാഖണ്ഡത്തിലെ ഏതെങ്കിലും ബിന്ദുവിൽ നിന്നായിരിക്കും.
ഈ നാലു ബിന്ദുക്കളിൽ നിന്നുമുള്ള ദൂരങ്ങളുടെ തുക ഏറ്റവും കുറവാകണമെങ്കിൽ ആ ബിന്ദു ഈ രണ്ടു രേഖാഖണ്ഡങ്ങളിലും ഉണ്ടാവണം. അതായത് ആ സൈക്ലിക് ക്വാഡിലേറ്ററിന്റെ രണ്ടു വികർണ്ണങ്ങളുടെ സംഗമബിന്ദു.
| Attempts | 64 |
| Correct | 7 |
| Best Explanation | Umesh P Narendran |
First 10 Correct Answers
| Sl No | Primary | High School | Others |
| 1 | Eshan A | Neerad P K | Umesh P Narendran |
| 2 | Aman V Shankar | _ | Pranav D P |
| 3 | _ | _ | Anusha Ramesh. V |
| 4 | _ | _ | _ |
| 5 | _ | _ | _ |
| 6 | _ | _ | _ |
| 7 | _ | _ | _ |
| 8 | _ | _ | _ |
| 9 | _ | _ | _ |
| 10 | _ | _ | _ |
