

Solution:
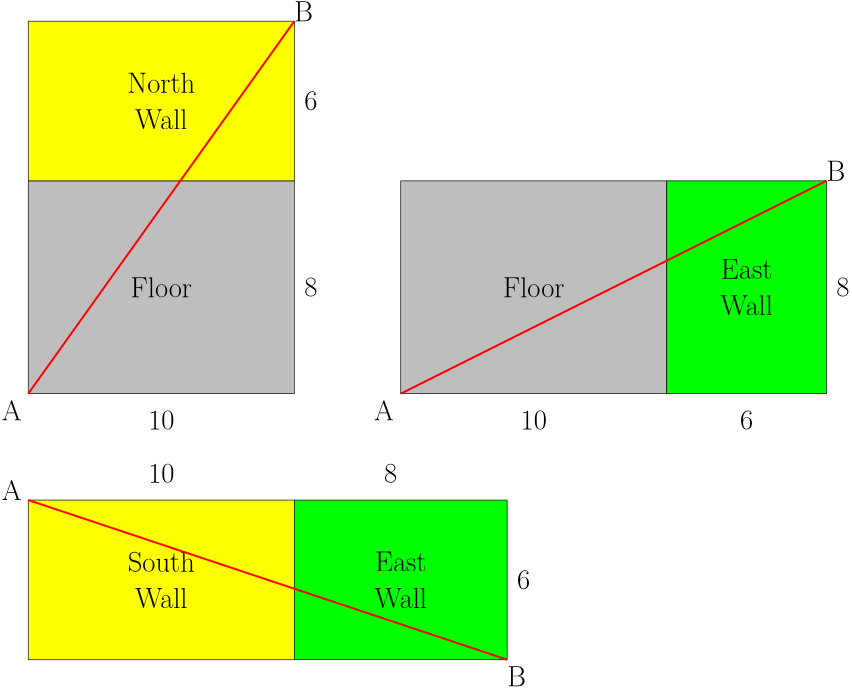
ഒരു കാർഡ് ബോർഡ് പെട്ടി പൊളിക്കുന്ന പോലെ മുറിയെ തുറന്നു പരത്തി വെച്ചാൽ A-യിൽ നിന്ന് B-യിൽ എത്താൻ മൂന്ന് നേർരേഖകൾ കാണാം. പൈത്തഗോറസ് സിദ്ധാന്തം പ്രകാരം ഇവയുടെ നീളങ്ങളുടെ സ്ക്വയർ (10+8)^2 + 6^2, (10 + 6)^2 + 8^2, (6 + 8)^2 + 10^2 എന്നിങ്ങനെയാണ്. ഈ മൂന്നിൽ ഏറ്റവും ചെറുത് മൂന്നാമത്തതാണ് (296). അതിനാൽ ദൂരം ഏതാണ്ട് 17.2m.
If you imagine that the room is a cardboard box and you cut open the box and lay it on a flat surface, you can see that there are three possible straight line paths from A to B. By Pythagoras theorem the length of their squares are (10+8)^2 + 6^2, (10 + 6)^2 + 8^2, and (6 + 8)^2 + 10^2. Out of the three, the third one is the smallest (296) and its square root is around 17.2m.
Best Explanation : Umesh P Narendran
43-ആം പസ്സിലിന്റെ എക്സ്റ്റൻഷനാണ് ഇത്. പെട്ടിയുടെ വശങ്ങൾ a, b, c എന്നിവയാണെന്നിരിക്കട്ടേ. പെട്ടിയെ പൊളിച്ച് നിരത്തി വെച്ചാൽ ഈ ദൂരം (a+b) നീളവും c വീതിയുമായ ഒരു ദീർഘചതുരത്തിന്റെ രണ്ട് എതിർമൂലകളാണെന്നു കാണാം .
അപ്പോൾ, ദൂരം = √(a+b)^2 + c^2 = √(a^2 + b^2 + c^2 + 2ab)
ഇത് ഏറ്റവും ചെറുതാക്കാൻ c-യ്ക്ക് ഏറ്റവും വലിയ വശത്തിന്റെ വില കൊടുക്കുക. c = 10, a = 6, b = 8.
ഉത്തരം = √(6+8)^2 + 10^2 =√(196 + 100) = √296 = 17.2.
| Attempts | 86 |
| Correct | 4 |
| Best Explanation | Umesh P Narendran |
First 10 Correct Answers
| Sl No | Primary | High School | Others |
| 1 | Aman V Shankar | Avinash | Umesh P Narendran |
| 2 | – | Anushka Shajith | – |
| 3 | – | – | – |
| 4 | – | – | – |
| 5 | – | – | – |
| 6 | – | – | – |
| 7 | – | – | – |
| 8 | – | – | – |
| 9 | – | – | – |
| 10 | – | – | – |
