

Solution:
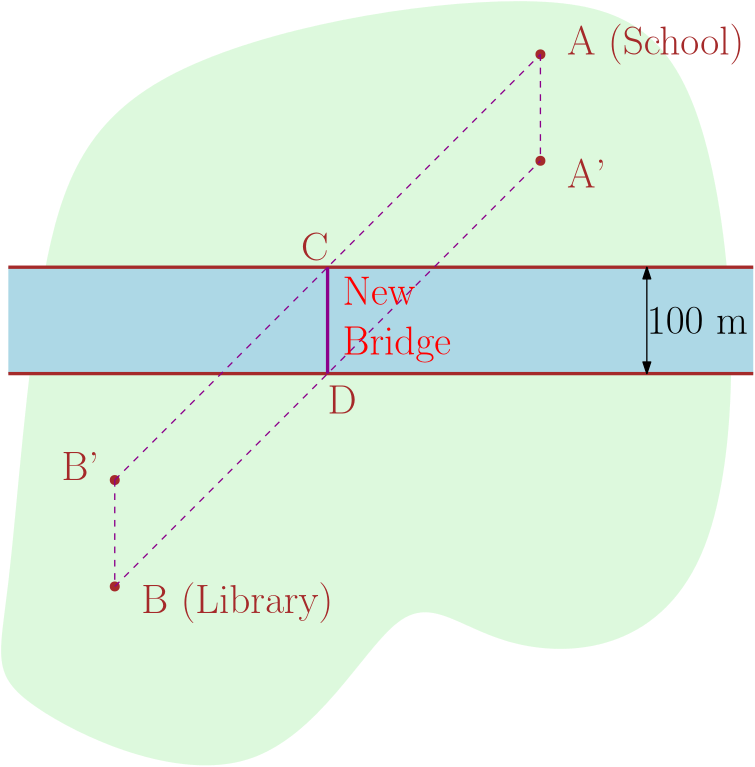
പാലത്തിന്റെ സ്കൂൾ അറ്റത്തെ C എന്നും അതിൻ്റെ ലൈബ്രറി അറ്റത്തെ D എന്നും വ്വിളിക്കാം. അപ്പോൾ മൊത്തം യാത്രാ ദൂരം AC + 100 + DB മീറ്ററാണ്. അതായത് യാത്രാദൂരം ഏറ്റവും കുറയുന്നത് AC + DB ഏറ്റവും കുറയുമ്പോളാണ്. പുഴയുടെ വീതി പൂജ്യം ആണെന്ന് ഒരു നിമിഷം സങ്കൽപ്പിക്കുക, അപ്പോൾ പാലം ചുരുങ്ങി ഒരൊറ്റ ബിന്ദുവായി (C = D) മാറുന്നു. ഈ പുതിയ ചിത്രത്തിൽ, AC + DB ഏറ്റവും കുറയുന്നത് C-യും D-യും ചെരുന്ന ആ ബിന്ദു) AB എന്ന നേർരേഖയിൽ വരുമ്പോളാണ്. ഇനി നിങ്ങൾ പുഴയെ അതിൻ്റെ യഥാർത്ഥ വീതിയിലേക്ക് വീതി കൂട്ടുന്നതായി സങ്കൽപ്പിക്കുകയാണെങ്കിൽ, ചിത്രത്തിൽ കാണിച്ചിരിക്കുന്നതുപോലെ C, D എന്നിവ വീണ്ടും വിഭജിക്കപ്പെടും. C എന്നത് AB’ എന്ന രേഖ നദിയുടെ സ്കൂൾ തീരത്തെ ഛേദിക്കുന്ന ബിന്ദുവാണെന്നും D എന്നത് A’B എന്ന രേഖ നദിയുടെ ലൈബ്രറി തീരത്തെ ഛേദിക്കുന്ന ബിന്ദുവാണെന്നും കാണാം. ഇവിടെ A, B എന്ന ബിന്ദുവിൽ നിന്നും നദിയിലേക്ക് 100 മീറ്റർ നീങ്ങിയാൽ എത്തുന്ന ബിന്ദുക്കളാണ് A’-ഉം B’-ഉം.
Let C be the school end of the bridge and D be its library end. The total travel distance is then AC + 100 + DB metres. Since the middle term (100) remains the same wherever you build the bridge, we should minimise AC + DB. Now imagine that you shrink the river to a line so that the whole bridge becomes a single point C = D. In this new picture, AC + DB is minimised when the common point (C = D) is on the straight line joining A and B. Now if you imagine widening the river back to its original width, C and D will split again as shown. In fact, C is the point where the line segment AB’ intersects the school bank of the river and D is the point where the line A’B intersects the library bank of the river. A’ and B’ are points you get if you move A and B 100 metres toward the river.
| Attempts | 109 |
| Correct | 1 |
First 10 Correct Answers
| First 10 Correct Answers | Primary | High School | Others |
| 1 | _ | _ | Umesh P Narendran |
| 2 | _ | _ | _ |
| 3 | _ | _ | _ |
| 4 | _ | _ | _ |
| 5 | _ | _ | _ |
| 6 | _ | _ | _ |
| 7 | _ | _ | _ |
| 8 | _ | _ | _ |
| 9 | _ | _ | _ |
| 10 | _ | _ | _ |
